벌들이 육각형을 사용하는 데에는 한 가지 간단한 이유가 있습니다. 바로 자연에서 건축에 가장 효율적인 모양이기 때문입니다. 육각형 격자는 가능한 최대의 저장 공간과 구조적 무결성을 가진 셀 격자를 만드는 데 가장 적은 양의 재료(이 경우 밀랍)를 사용합니다. 이는 수백만 년의 진화를 통해 다듬어진 완벽한 해결책입니다.
벌집의 육각형은 무작위적인 선택이 아닙니다. 복잡한 공학적 문제에 대한 수학적으로 최적화된 해결책입니다. 이는 건축 자재 최소화, 저장 용량 최대화, 구조적 안정성 보장 사이의 완벽한 절충안을 나타냅니다.
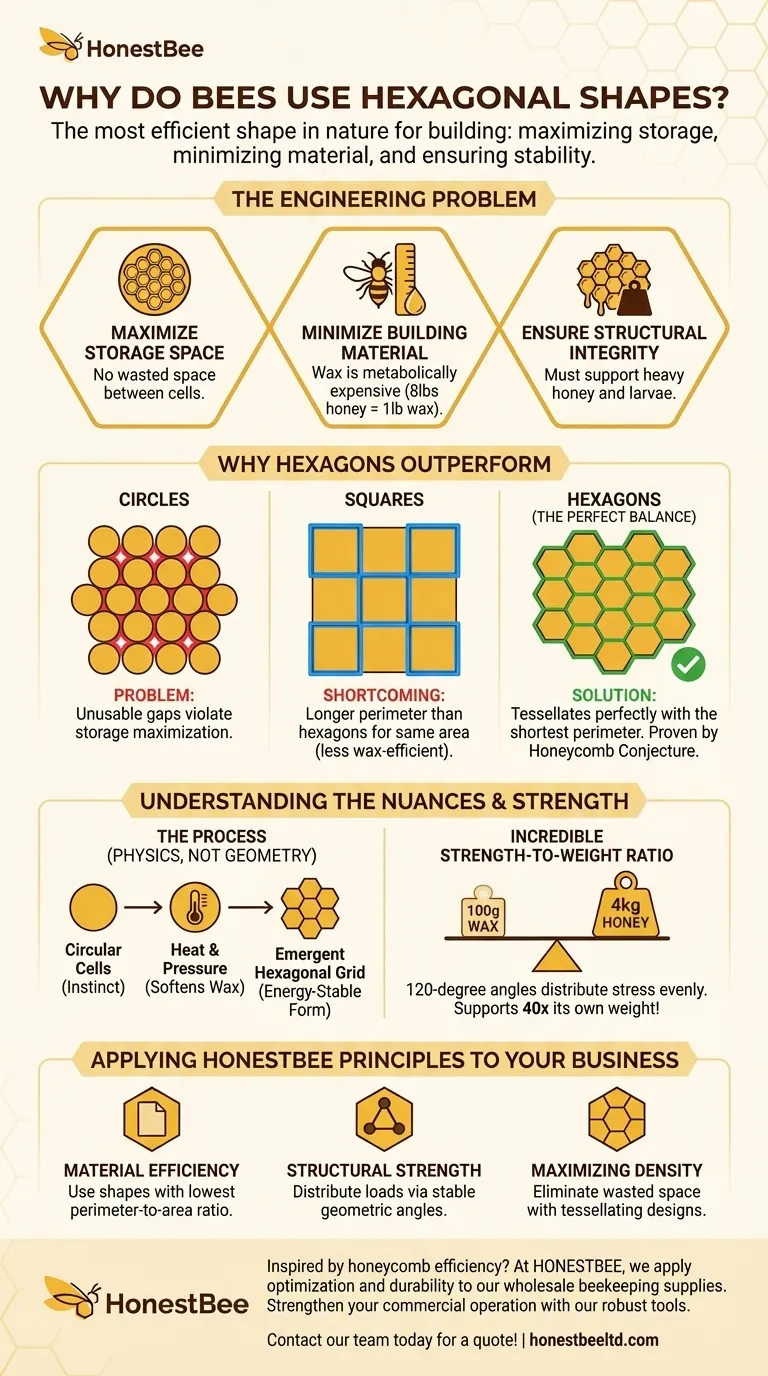
벌들이 해결해야 할 공학적 문제
육각형의 천재성을 이해하려면 먼저 벌들이 직면한 과제를 이해해야 합니다. 그들은 세 가지 중요한 공학적 요구 사항을 충족하는 구조가 필요합니다.
저장 공간 극대화
군집의 생존은 가능한 한 많은 꿀과 꽃가루를 저장하는 데 달려 있습니다. 따라서 저장 셀의 모양은 낭비되는 틈 없이 공간 효율적이어야 합니다.
건축 자재 최소화
벌들은 밀랍 1파운드를 생산하기 위해 약 8파운드의 꿀을 소비해야 합니다. 이로 인해 밀랍은 비효율적인 설계에 낭비될 수 없는 대사적으로 비용이 많이 드는 자원이 됩니다. 이상적인 모양은 가장 짧은 둘레로 주어진 면적을 둘러싸야 합니다.
구조적 무결성 보장
완성된 벌집은 믿을 수 없을 정도로 무겁습니다. 이 구조는 꿀의 무게뿐만 아니라 발달 중인 애벌레의 무게를 지탱할 만큼 충분히 강해야 하며, 동시에 비교적 부서지기 쉬운 재료로 만들어져야 합니다.

다른 모양보다 육각형이 뛰어난 이유
이러한 필요에 비추어 평가할 때, 육각형은 모든 조건을 완벽하게 충족하는 유일한 모양으로 두드러집니다. 원이나 정사각형과 같은 다른 일반적인 모양에는 심각한 결함이 있습니다.
원의 문제점
원은 기술적으로 둘레가 가장 짧으면서 가장 많은 면적을 차지하는 가장 효율적인 모양입니다. 그러나 원을 서로 밀착시키면 사용할 수 없는 틈이 생겨 저장 공간을 최대화해야 한다는 요구 사항을 위반합니다.
정사각형의 단점
정사각형, 삼각형, 육각형은 틈 없이 평평한 표면에 꼭 맞을 수 있는 유일한 정다각형입니다. 정사각형은 틈새 문제를 해결하지만, 동일한 면적을 둘러싸는 데 육각형보다 더 긴 둘레가 필요하므로 밀랍 효율성이 떨어집니다.
육각형의 완벽한 균형
육각형은 완벽하게 틈 없이 맞물리면서 그렇게 할 수 있는 어떤 모양보다도 둘레가 가장 짧기 때문에 우수한 선택입니다. 이 원칙은 1999년 "벌집 추측(Honeycomb Conjecture)"에서 수학적으로 증명될 정도로 근본적입니다. 이는 최소한의 재료 비용으로 최대의 저장을 제공하는 이상적인 중간 지점입니다.
절충점과 뉘앙스 이해하기
벌집의 완벽한 기하학을 감탄하지만, 그 과정은 벌들이 뛰어난 건축가라는 것보다는 물리학을 활용하는 것에 가깝습니다.
의식적인 기하학이 아닙니다
벌들은 의식적으로 각도를 측정하지 않습니다. 이 육각형 구조는 본능과 물리적 힘에 의해 주도되는 창발적 속성입니다. 벌들은 서로 가까이 대략 원형의 셀을 만듭니다.
열과 압력의 힘
벌들의 몸에서 발생하는 열이 밀랍을 부드럽게 만듭니다. 주변 셀의 표면 장력과 압력이 원형 구조를 가능한 가장 에너지적으로 안정적이고 압축된 형태, 즉 완벽한 육각형 격자로 끌어당깁니다.
놀라운 강도 대 중량 비율
최종 구조는 효율적인 설계의 증거입니다. 셀 벽이 만나는 120도 각도는 응력을 고르게 분산시키는 데 이상적입니다. 이로 인해 무게가 100그램에 불과한 벌집이 최대 4킬로그램의 무게를 지탱할 수 있게 되는데, 이는 자연 공학의 놀라운 성과입니다.
프로젝트에 적용하는 방법
벌집 설계의 원리는 벌에만 국한되지 않습니다. 이는 공학, 설계 및 물류에 강력한 교훈을 제공합니다.
- 주요 초점이 재료 효율성인 경우: 타일링할 수 있는 모양 중에서 둘레 대 면적 비율이 가장 낮은 모양을 사용하며, 육각형이 이상적인 선택입니다.
- 주요 초점이 구조적 강도인 경우: 벌집처럼 공유 벽과 안정적인 기하학적 각도를 통해 하중을 분산시키십시오.
- 주요 초점이 밀도 극대화인 경우: 설계가 단위 사이에 낭비되는 공간을 제거하도록 모양이 틈 없이 맞물리도록 하십시오.
벌집은 최적화의 마스터클래스로 서 있으며, 단순한 물리적 원리가 어떻게 놀라울 정도로 견고하고 효율적인 구조를 만들어낼 수 있는지 보여줍니다.
요약표:
| 요구 사항 | 육각형이 뛰어난 이유 |
|---|---|
| 저장 공간 최대화 | 완벽하게 틈 없이 맞물려 셀 사이에 낭비되는 공간이 전혀 없습니다. |
| 재료(밀랍) 최소화 | 틈 없이 맞물리는 모든 모양 중에서 둘레 대 면적 비율이 가장 짧습니다. |
| 구조적 무결성 보장 | 120도 각도가 응력을 고르게 분산시켜 놀라운 강도를 제공합니다. |
벌집의 효율성에 감명받으셨습니까? HONESTBEE에서는 양봉 용품에 최적화 및 내구성의 동일한 원칙을 적용합니다. 우리는 상업 양봉장과 양봉 장비 유통업체에 강력하고 고품질의 도구를 제공하여 강력하고 생산적인 운영을 구축할 수 있도록 지원합니다. 도매 중심 솔루션이 귀하의 비즈니스를 어떻게 강화할 수 있는지 논의해 봅시다. 견적을 받으려면 오늘 저희 팀에 문의하십시오!
시각적 가이드
관련 제품
- 수동 밀랍 빗 파운데이션 기계 왁스 파운데이션 밀 엠보싱 기계
- 식품 등급 꿀벌 프레임용 플라스틱 꿀벌 파운데이션
- 밀랍 파운데이션 시트 벌집 파운데이션 도매용
- 작동 트레이와 왁스 파운데이션 롤러가 있는 전동 밀랍 파운데이션 기계
- 전문적인 프레임 준비: 허니스트비 전선 임베더



















